안녕하세요. 개발자 엄탱입니다.
이 글은 알고리즘을 공부하면서 공부 기록용입니다.
그래서 설명마다 일기용으로 편하게 작성하여 반말 형식으로 작성하려고 합니다.
그리고 보시다가 더 좋은 방법이나 잘 못 알고 있는 내용이 있다면 알려주시면 정말 감사하겠습니다.
좋은 하루 되세요 :)
이번 문제는 백준 7040번 밥먹기 플래티넘1 문제 인데, 난이도에 비해 어렵지 않게 풀 수 있는 문제이지만, 만약 알고리즘 분류에 벨만-포드를 보고 벨만-포드 알고리즘으로 접근해서 쉽게 풀렸지만, 만약 어떤 알고리즘으로 사용해야 하는지 몰랐으면 못 풀었을 것 같다.
문제
소들은 밥을 먹을 때 친구들과 가까이 줄을 선다. 선영이는 소를 N마리 (2 ≤ N ≤ 1,000 가지고 있고, 1번부터 N번까지 번호를 붙였다. 소는 일직선으로 번호 순으로 줄을 서서 밥을 기다린다. 이때, 두 마리 이상의 소가 같은 위치에 서는 것도 가능하다. 같은 좌표를 갖는 소가 두 마리 이상일 수도 있다.
서로를 좋아하는 소는 특정 거리 이내에 서 있으려고 한다. 그리고 서로를 싫어하는 소는 특정 거리 이상 떨어지려고 한다. 어떤 소들이 서로를 좋아하는지와 두 소가 최대한 떨어질 수 있는 거리가 길이가 ML(1 ≤ ML ≤ 10,000)인 리스트로 주어진다. 다음으로 어떤 소들이 서로를 싫어하는지와 두 소가 최소한 떨어져야 하는 거리가 MD(1 ≤ MD ≤ 10,000) 길이의 리스트로 주어진다.
위 조건을 만족하면서 줄을 서는 것이 가능하다면, 1번 소와 N번 소의 최대 거리를 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에는 정수 N, ML, MD가 공백으로 구분되어 주어진다.
둘째 줄부터 ML+1번째 줄까지 양의 정수 A, B, D (1 ≤ A < B ≤ N)가 공백으로 구분되어 주어진다. 소 A와 소 B는 최대한 D (1 ≤ D ≤ 1,000,000)만큼 떨어질 수 있다.
ML+2번째 줄부터 ML+MD+1번째 줄까지 양의 정수 A, B, D (1 ≤ A < B ≤ N)이 공백으로 구분되어 주어진다. 소 A와 소 B는 최소한 D (1 ≤ D ≤ 1,000,000)만큼 떨어져 있어야 한다.
출력
첫째 줄에 1번 소와 N번 소의 최대 거리를 출력한다. 줄을 서는 것이 불가능한 경우에는 -1을 출력한다. 1번 소와 N번 소의 최대 거리가 무한대인 경우에는 -2를 출력한다.
예제 입력 1
4 2 1
1 3 10
2 4 20
2 3 3예제 출력 1
27알고리즘 분류
- 그래프 이론
- 그리디 알고리즘
- 벨만-포드
문제 설명
이 문제는 간단하게 1번 부터 N번의 소가 일직선상에 서 있을 때, 1번에서 N번의 최대 거리를 구하는 문제이다.
여기서 1번에서 N번의 최대거리가 무한대인 경우엔 -2를 출력하고, 줄을 서는 것이 불가능한 경우(음수 사이클) -1을 출력하면 된다.
- 최대 거리가 무한대인 경우는 예를 들어 1번과 2번의 최대 거리가 없고 최소 거리만 있으면 둘의 거리의 제한은 무한대가 되어 진다.
- 줄을 서는 것이 불가능한 경우는 예를 들어 아래와 같은 경우 일 때 일어난다.
A와 C가 최소 거리가 3이 되어야 하는데 최대거리를 아무리 늘려봐야 2밖에 안된다.
즉, A와 C의 최대거리 - A와 C의 최소거리가 음수가 나오면 불가능한 경우이므로, 음수 사이클이면 불가능하다고 판단할 수 있는 것이다.
- A소, B소의 최대거리(ML) 1
- B소, C소의 최대거리(ML) 1
- A소, C소의 최소거리(MD) 3
- 두 가지 경우 외에는 최대 거리를 출력하면 된다.
해설(해설 요약해 놓은 것만 봐도 괜찮을 듯하다.)
이 문제는 구현이 어렵지 않고 어떤 식으로 ML과 MD의 값을 관계를 지어줄까만 생각해 내면 풀어 낼 수 있는 문제이다.
처음에 이 문제를 접근할 때, 노트에 써서 어떤식으로 관계가 될 수 있을지 그려보면서 생각해봤다.
위의 예제로 설명해 보겠다.
4 2 1 (소의 수, ML 리스트 수, MD 리스트 수)
1 3 10 (ML - 좋아하는 소끼리의 최대 거리)
2 4 20 (ML - 좋아하는 소끼리의 최대 거리)
2 3 3 (MD - 싫어하는 소끼리의 최소 거리)
아래는 ML의 거리만 나타낸 거다.
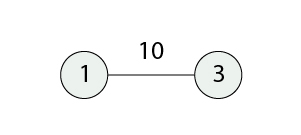

아래는 ML과 MD의 거리를 합친 그림이다.

보면 소2는 일직선상에 놓이기 때문에 소1과 소3 사이 어딘가에 배치되어야 한다.
여기서 소2와 소3의 최소거리가 주어지기 때문에, 소2의 최대 거리는 소3의 최대 거리 - 소2와 소3의 최소거리가 된다.
여기서 중요한건 2정점 -> 3정점 -3으로 생각하면 안 된다.
3정점이 2정점보다 오른쪽에 있으니까, 3정점 -> 2정점 -3으로 생각해야 한다.
여기서 소1과 소3의 ML 값이 없다고 가정한다면, 1과 3의 거리가 무한대로 되고 2는 그 사이 어딘가(소2의 최대거리 <= 소3 최대거리 - 3)에만 배치되면 되니까 결국, 1과 4는 무한대가 된다.
해설 요약
- ML은 A소에서 B소까지의 거리값으로 정리하고 MD는 B소에서 A소까지의 음수 거리값으로 정리
- N까지의 거리가 처음에 설정한 INF(엄청 큰 값)이라면 -2 출력, 음수 사이클이 발견되면 -1을 출력
- 그 외에는 최대 거리값 출력
import java.io.BufferedWriter;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
static BufferedReader br;
static StringTokenizer st;
static int N;
static int ML;
static int MD;
static long INF = Long.MAX_VALUE;
static ArrayList<Edge> edge;
static long[] distDp;
public static void main(String[] args) throws Exception {
br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
ML = Integer.parseInt(st.nextToken());
MD = Integer.parseInt(st.nextToken());
edge = new ArrayList<>();
distDp = new long[N + 1];
Arrays.fill(distDp, INF);
distDp[1] = 0;
for (int i = 0; i < ML; i++) {
st = new StringTokenizer(br.readLine(), " ");
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int dist = Integer.parseInt(st.nextToken());
edge.add(new Edge(from, to, dist));
}
for (int i = ML; i < ML + MD; i++) {
st = new StringTokenizer(br.readLine(), " ");
int to = Integer.parseInt(st.nextToken());
int from = Integer.parseInt(st.nextToken());
int dist = Integer.parseInt(st.nextToken());
edge.add(new Edge(from, to, -dist));
}
boolean minusCycle = bellmanFord();
if (!minusCycle) {
bw.write(-1 + "\n");
} else if (distDp[N] == INF) {
bw.write(-2 + "\n");
} else {
bw.write(distDp[N] + "\n");
}
bw.flush();
bw.close();
br.close();
}
public static boolean bellmanFord() {
for (int i = 0; i < N + 1; i++) {
for (int j = 0; j < edge.size(); j++) {
Edge cur = edge.get(j);
if (distDp[cur.from] != INF
&& distDp[cur.to] > distDp[cur.from] + cur.dist) {
distDp[cur.to] = distDp[cur.from] + cur.dist;
if (i == N) {
return false;
}
}
}
}
return true;
}
}
class Edge {
int from;
int to;
int dist;
Edge(int from, int to, int dist) {
this.from = from;
this.to = to;
this.dist = dist;
}
}코드 설명 (생략 가능)
우선 코드를 보면 distDp 배열의 자료형과 INF값을 long으로 잡았는데, 이유는 문제의 데이터들 각각 최대로 잡으면 int 최댓값을 넘어갈 것 같아서 위와 같이 long 자료형으로 했다.
하지만 내가 생각한 게 맞을까 하고 int자료형으로 다 바꿔서 실행을 했는데 정답이라고 나온다.
이 부분은 좀 더 생각해봐야겠다.
아니면 테스트 케이스들 중에 데이터가 최대로 되어있는 경우가 없어서 통과되는 것일 수 있다.
우선 long으로 하는 게 더 정확한 것 같다.
결과 (생략 가능)
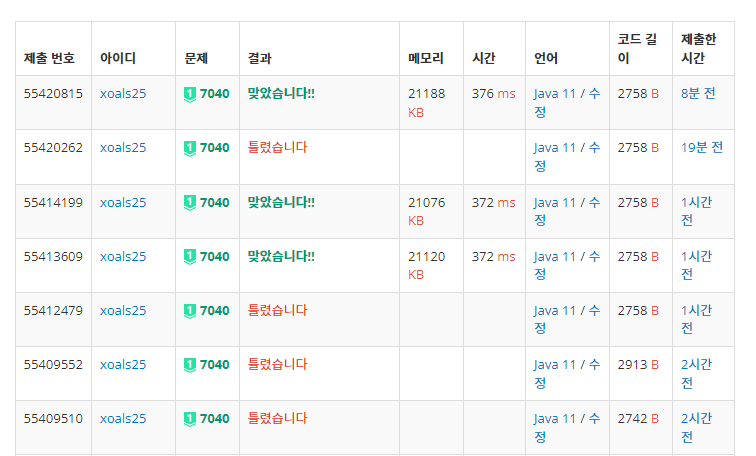
처음에 틀렸던 이유가 -1, -2 출력 조건을 반대로 해서 틀렸다 바꿔주니 바로 맞았다.
그리고 int자료형, long자료형을 변경해서 채점해 보면 둘 다 맞았다고 나왔다.
'알고리즘 > 최단 경로' 카테고리의 다른 글
| [자바]백준 16958번 텔레포트 [그래프 - 플로이드 워셜][엄탱] (1) | 2023.02.10 |
|---|---|
| [자바]백준 11581번 구호물자 [그래프 - 플로이드 워셜][엄탱] (3) | 2023.02.08 |
| [자바]백준 1865번 웜홀 [그래프 - 벨만포드][엄탱] (2) | 2023.02.06 |
| [자바]백준 11657번 타임머신 [그래프 - 벨만 포드][엄탱] (4) | 2023.02.05 |
| [자바]백준 13549번 숨바꼭질3 [그래프-다익스트라][엄탱] (3) | 2023.02.03 |

